[ Martingale Trading Simulation Program, in BASIC (part1 of 2) - Jan. 13, 2026 ]

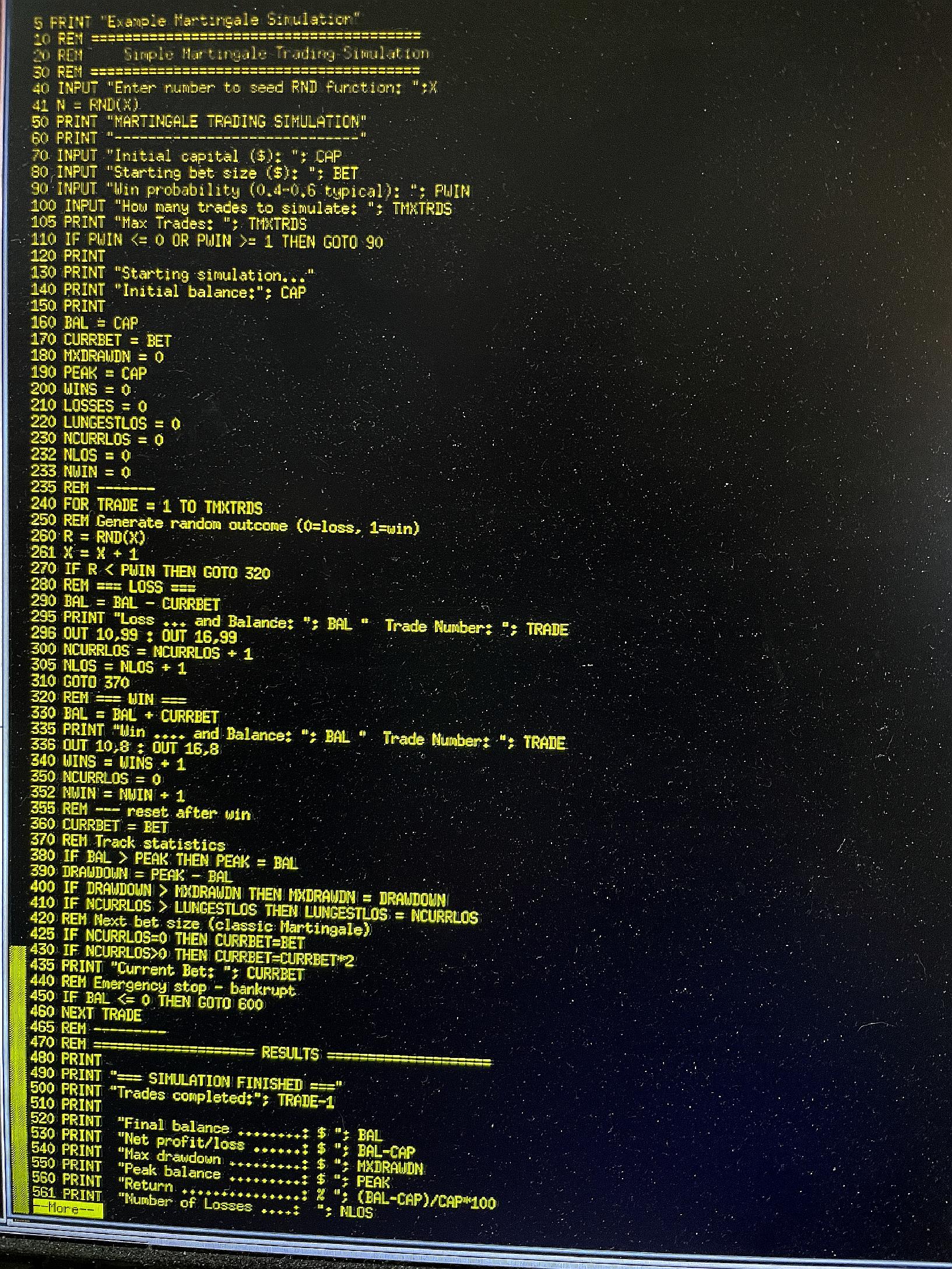
I asked the Grok.com AI to write a Martingale Trading Simulation program, in BASIC, so I could run it on my homemade Z80 SBC (Single Board Computer), which has a BASIC interpreter. There were some curious logic errors, but for the most part, the program was fully written, and with some debugging and fixes, and some extra display information as the program runs (so I can see how it is trading, and the bets it is making) the program is a fun exercise to experiment with.
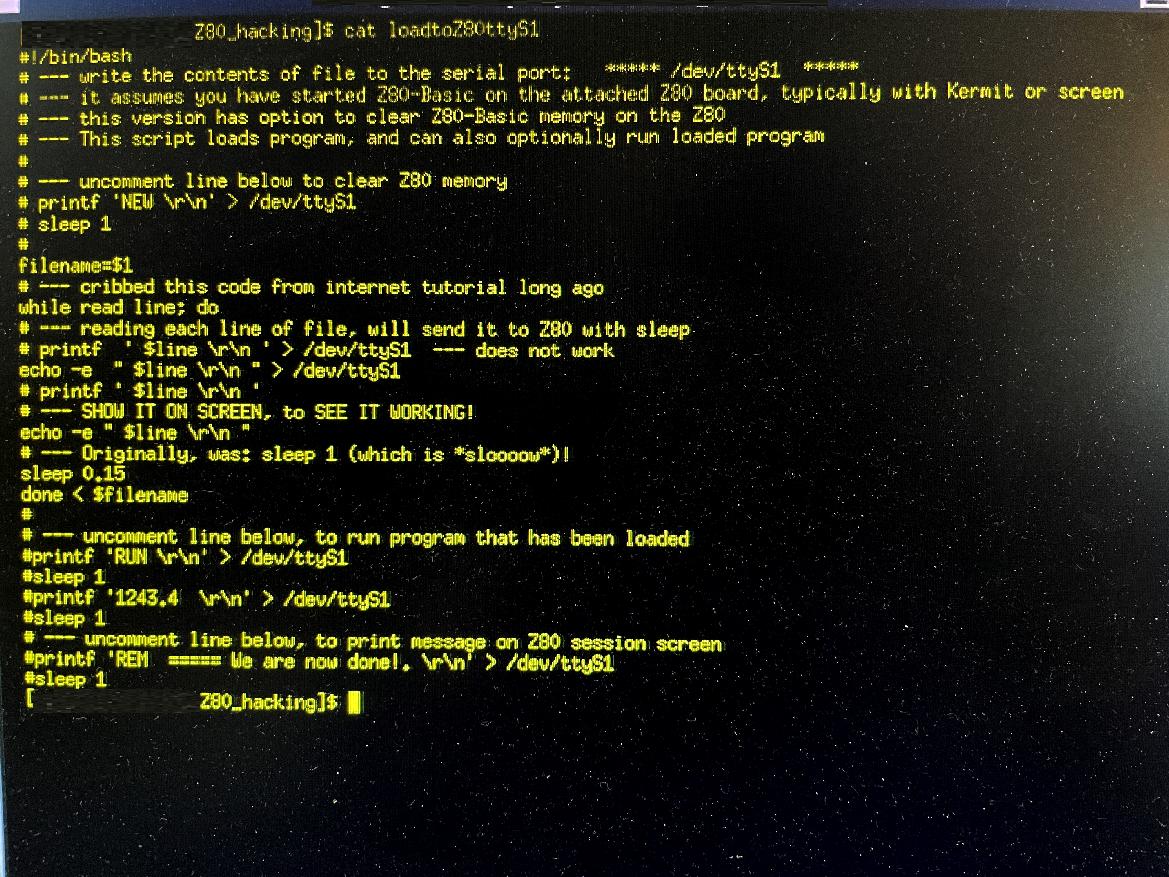
This screen shot shows the first part of the program. Below, is the image of rest of program. (Click on image to expand, ESC or click outside image to exit)

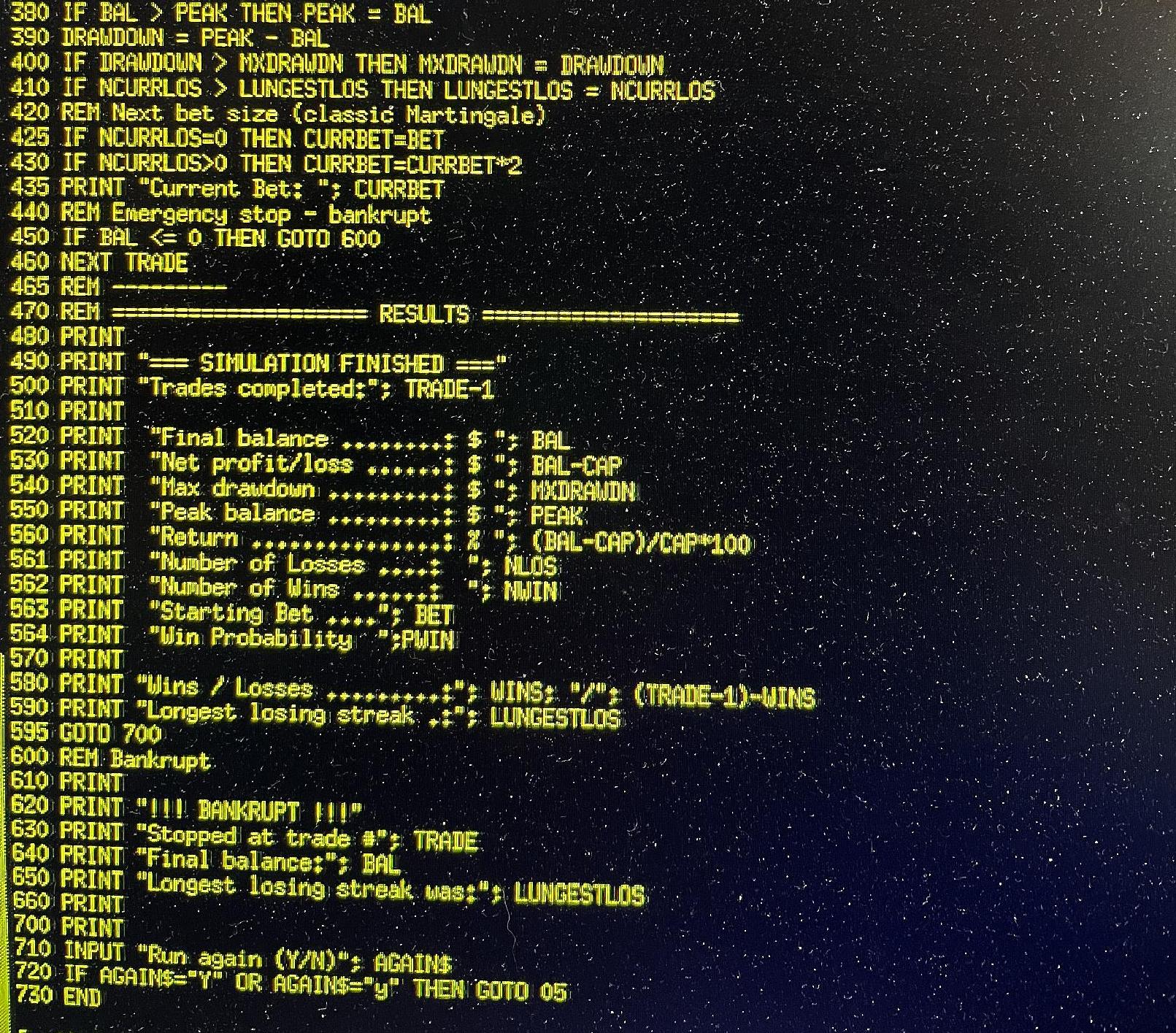
[ Martingale Trading Simulation Program, in BASIC (part-2) - Jan. 13, 2026 ]

This screen shot shows the second part of the program. Please excuse the awful resolution, which looked much better on the iPhone image. I will try to find time to clean this image up at some point. (Click on image to expand, ESC or click outside image to exit)

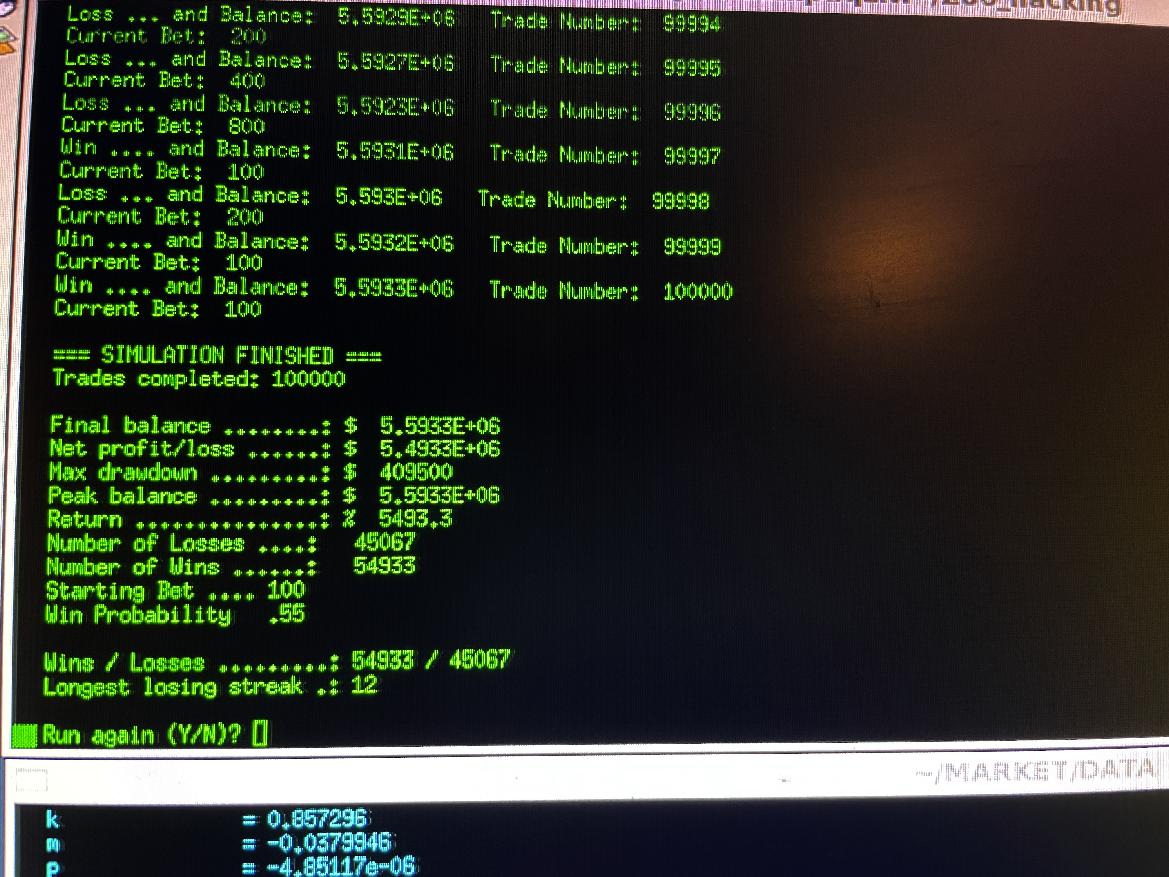
[ Martingale Trading Simulation Program, Run of 100,000 trades - Jan. 13, 2026 ]

This shows image of the Martingale Trading Simulator results, which was run on the Z80 SBC (Single Board Computer). The little program in file MARTINGL.BAS is loaded using a simple shell script, with "loadtoZ80ttyS1 MARTINGL.BAS" which assumes that you have used Kermit to connect to the Z80, and have started the Z80-Basic interpreter. The BASIC commands LIST and RUN are used to list the program, and then run it, respectively. As it is running, you can use "Ctrl-s" and "Ctrl-q" to pause and then continue the running simulation. You can see in this simulation, with starting capital of $100,000, and initial bet size of $100, the Martingale system ran the capital balance up to $5,593,300. But note the drawdown of $409,500! This was the result after 100,000 trades. Note there was a run of 12 losses in a row.
(Click on image to expand, ESC or click outside image to exit)

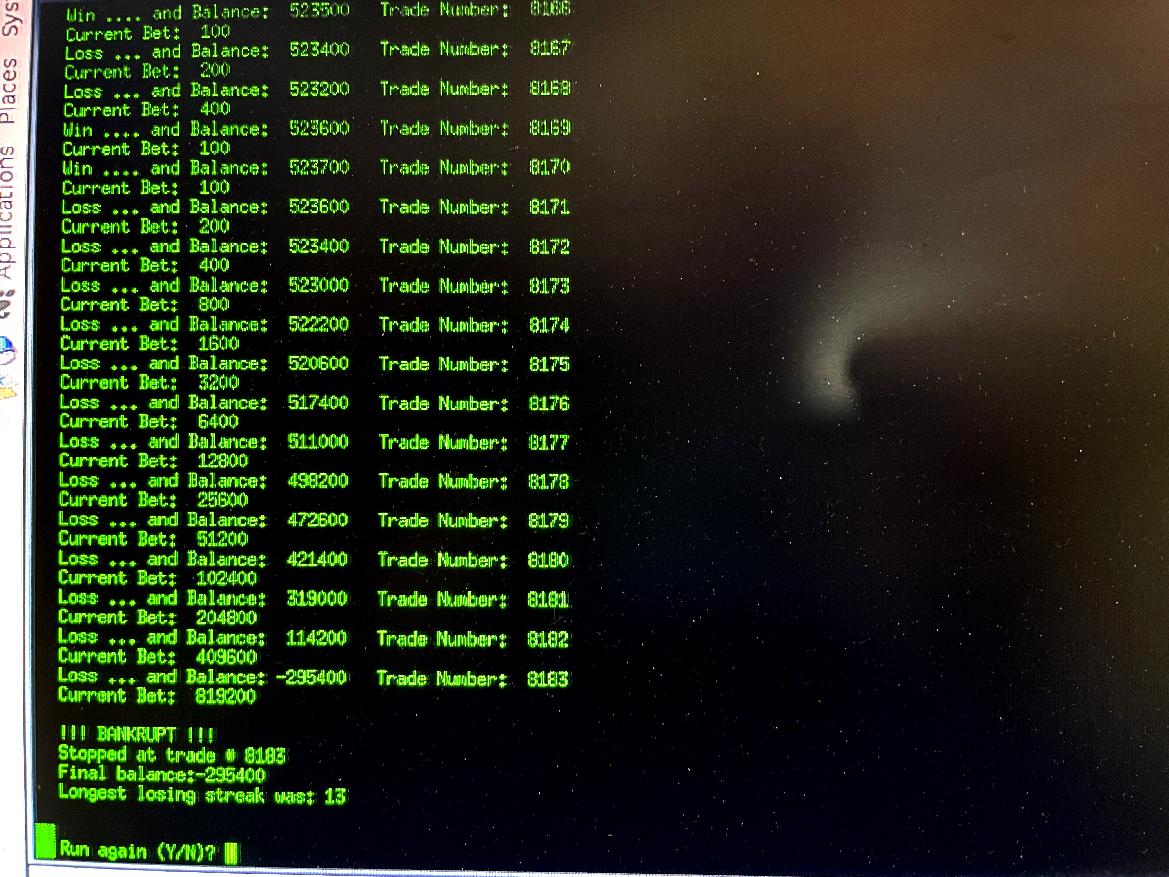
[ Martingale Trading Simulation Program, Run of 10,000 Trades - Jan. 13, 2026 ]

This shows image shows results of the Martingale Trading Simulator on a second run of 10,000 trades. The same parameters were used, but here we got a run of 13 losses in a row. The trading capital goes from $522,220 down to a $-295,400 balance. The simulated trader lost all his capital, and quite a bit more, because the system required a $409,600 bet be made to recover the string of losses. But it did not work, and generated a loss so large that capital went to negative $295,400. With the use of margin, these kinds of results are actually possible.

This run highlights the risk of the Martingale strategy.
The key thing to realize, is that the probability of win and the probability of loss is the same, each time. A long string of losses in a row, is a very low probability event, but it can occur, and it does occur. If your loss probability is 0.48, then the probability of 12 losses in a row, is 0.48 ** 12, which is a small value of 0.00014959. But in a run of 10,000 trades, that means that you can expect roughly 1.5 events of this type, and so one event of this low likelyhood is actually expected to occur, roughly once in 10,000 times. And in this run, it does, and the trader is wiped out, just like happened to the folks following "Captain Condor".

I think a *lot* of market actively is following strategies that are not dis-similar from this "Martingale" betting strategy. There is more risk in modern markets, than we can see. It only shows up very rarely, but it does show up.
(Click on image to expand, ESC or click outside image to exit)

[ The "loadtoZ80ttyS1" Program which is used to load BASIC program onto the Z80 SBC - Jan. 13, 2026 ]

This little program is a BASH shell script that takes any filename, and loads it line by line, to the Z80 (or any serial device attached to the Linux P/C serial port, and has a slight pause, sufficient to allow the Z80-Basic to save and register each line of the program. This little script works really well, and with it, and the Kermit "log session FILENAME.BAS" feature of Kermit (which lets you just capture the contents of a Kermit session, and write it to a file), one can load program to the Z80, and save them from the Z80, into Linux files on any Linux machine.

Kermit can be built on any Linux, if one has a C-compiler (I used gcc 4.8.5 on an old Linux box to build and install Kermit). To save the Basic program from Z80 to a Linux file, one escapes from the Z80 Kermit session with "ctrl-/" and "c", to "C-Kermit:", enters "log session FILENAME.BAS", returns to Kermit with "connect", enter "LIST" to list the whole program, then "ctrl-/" and "c" again to return to "C-Kermit:" prompt, and enter "close session".

The Basic program will be in file called "FILENAME.BAS". This little shell script shown here, can be run from a shell sub-session, from the "C-Kermit:" prompt as follows: Make the link to the Z80 with: the three commands at "C-Kermit:" prompt: "set line /dev/ttyS1", "set baud 38400", "set carrier-watch off" and then "connect". This connects to the Z80 serial port (you have to use a null-modem cable, which switches the RS-232 transmit and receive lines).

You boot Z80-Basic with "B", and then return to "C-Kermit:" prompt by entering the escape sequence ("ctrl-/" and "c"), and then enter "push" to get to a shell sub-session, and enter "./loadtoZ80ttyS1 MARTINGL.BAS" to load the Martingale Trading Simulator.

When it's done (you see each program line load, in the Linux command line shell), enter "exit" to close the BASH shell, and return to "C-Kermit:", where you enter "connect" to return to the Z80, and you will see your program. You run it with the Basic "RUN" command, and enter the trading simulation parameters, for capital, bet-size, number-of-trades. Note that you also must enter a random number to seed the pseudo-random-number generator. (Click on image to expand, ESC or click outside image to exit)

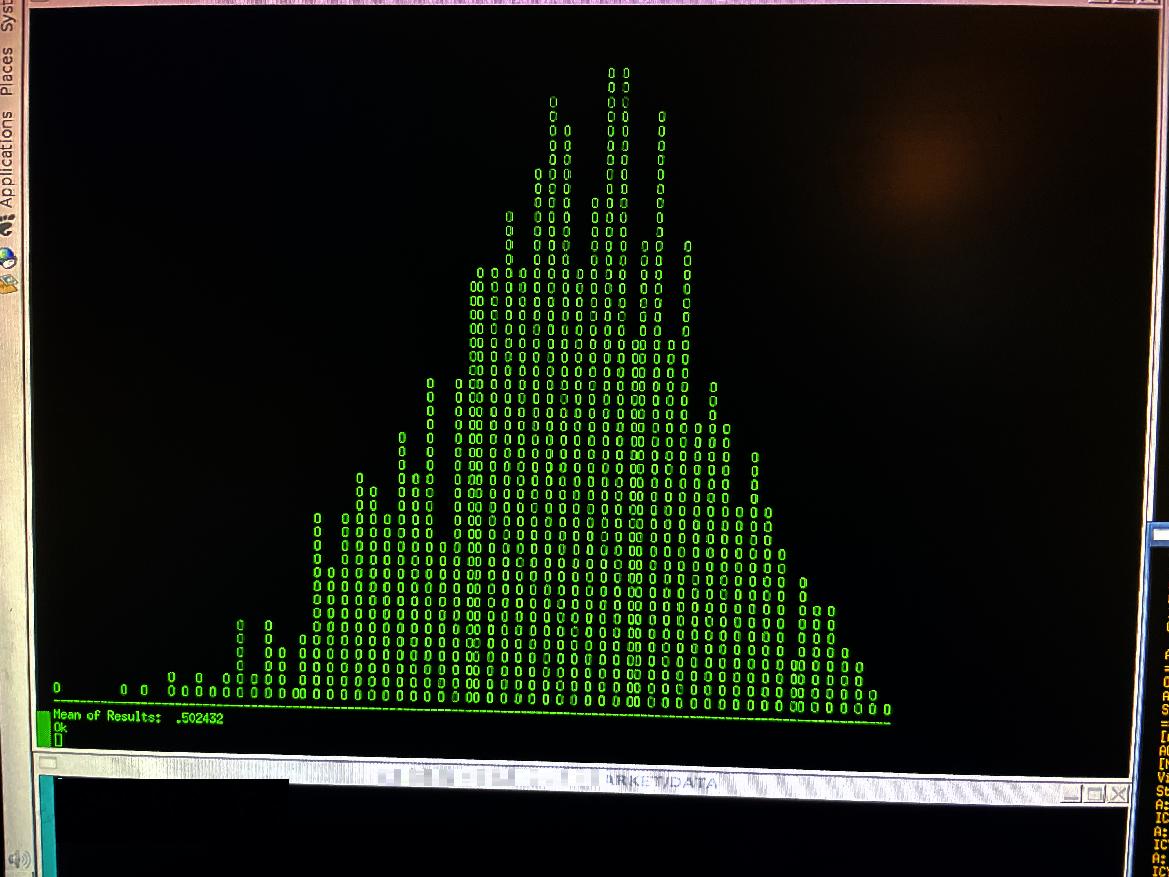
[ Randomness Generator Check Resulting Histogram - Jan. 15, 2026 ]

I wrote this program to check the quality of the pseudo-random values that the RND(x) function generates. The RND function is "seeded" with an initial value, each time the program is run, so that a different evolutionary path of results is generated. It is very difficult to get randomness on a computer, since anything you do, will tend to be deterministic. You have to have some confidence in your pseudo-random results being generated.

To check the RND function, I wrote a program that can generate arbitrarily sized boxes, filled with dots and spaces, and then count the number of dots for each trial, and produce a scaled average between 0 and 1.

This nice histogram shows all is pretty good. I had the program generate 1000 boxes of 5 rows by 80 columns, and "randomly" wrote either a dot or a space in each cell. Then, for each box, I range-scaled the result onto a 130 column by 80 row histogram display. One should get a nice bell-curve (a "Gaussian" curve), with a mean value around 0.50. And this is pretty much what we get, so it means I can trust the quality of the pseudo-random numbers, as being close enough to random, for any simulator which needs random outcomes, to work correctly.

(Click on image to expand, ESC or click outside image to exit)

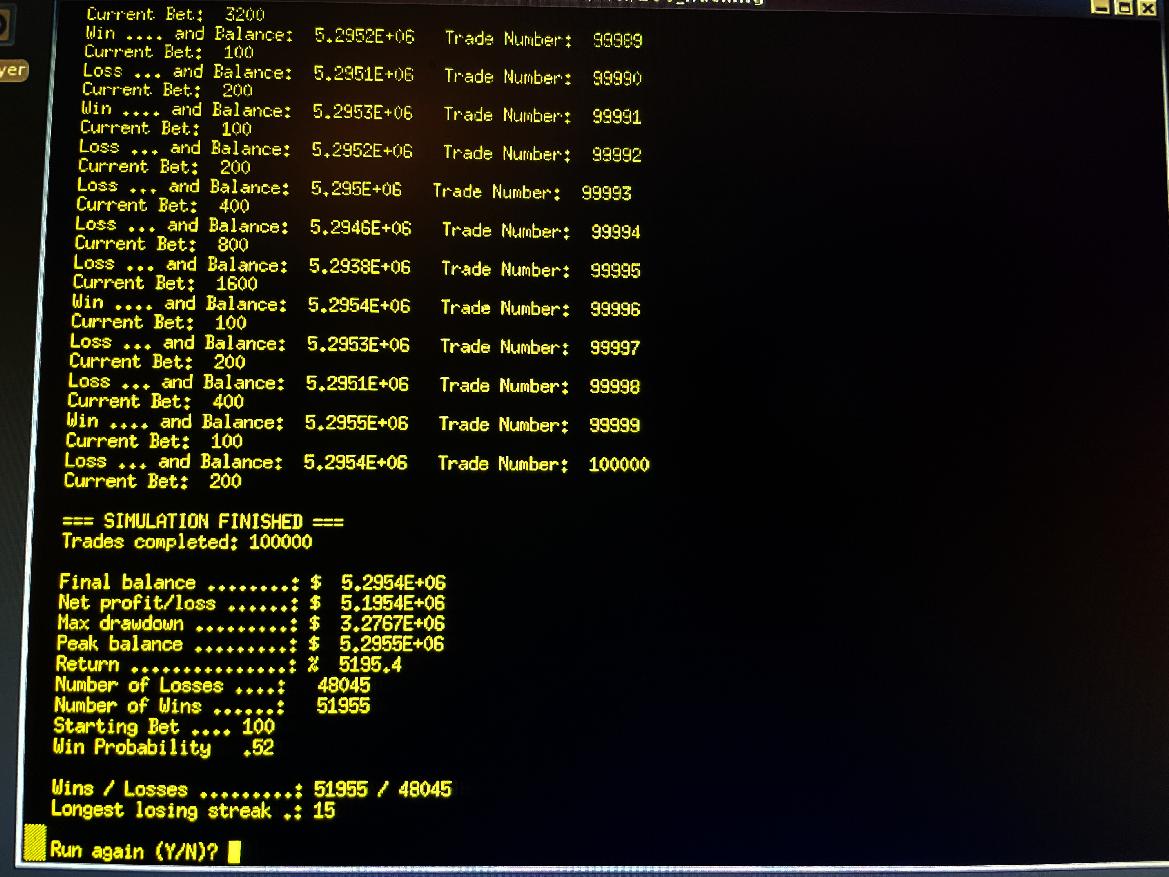
[ The Martingale Simulator Making 5 Million Dollars - Jan. 15, 2026 ]

Here is screen-shot of final run result of Martingale Simulator making over 5 million dollars, starting with 100,000 dollars, and an initial bet-size of $100, and a win probability of 0.52 (a very small edge), and 100,000 trades.

Note the there is a drawdown of over 3 million dollars, and a run of 15 losses in a row. Could any human make (and lose) a 7 figure bet, and withstand the 15 losses in a row?

Probably not.

There are reasons why this strategy is difficult to put into practice, despite the successful runs it can have. (Click on image to expand, ESC or click outside image to exit)

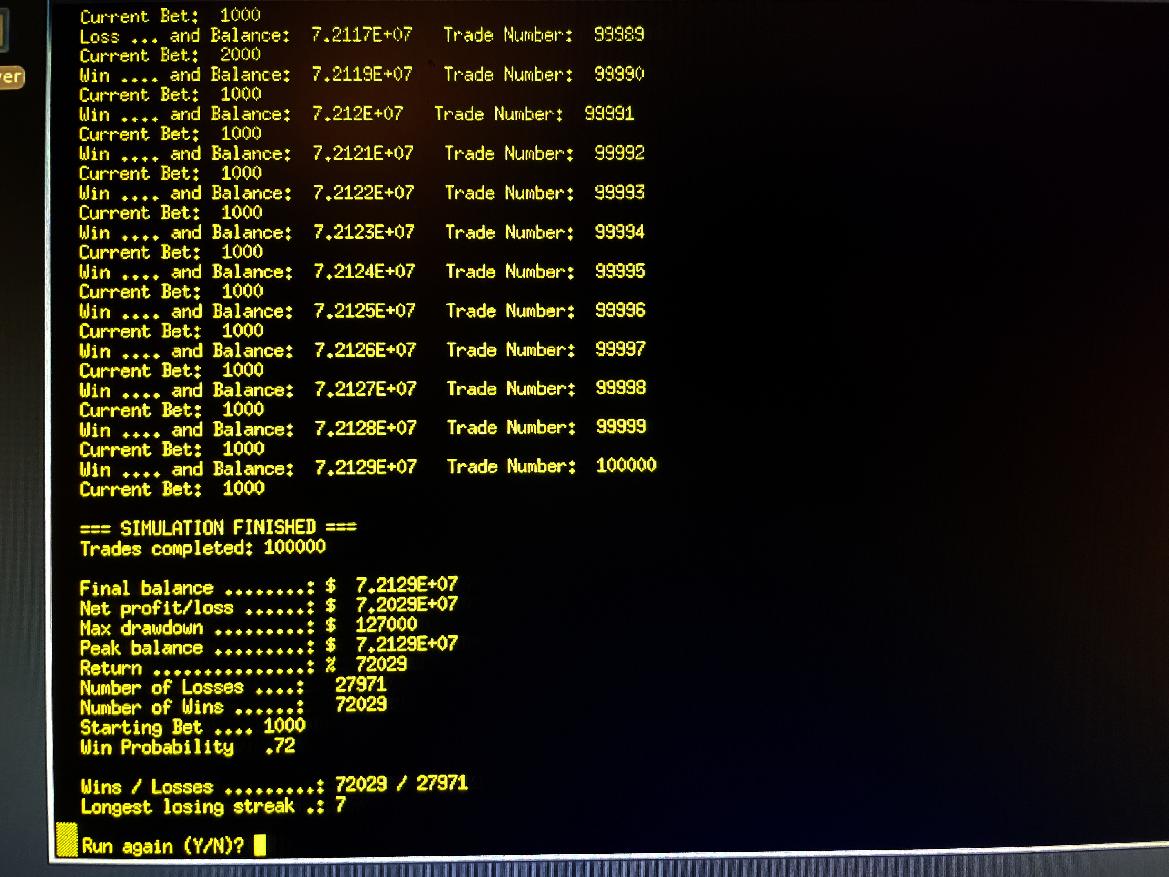
[ The Martingale Simulator Making 72 Million Dollars - Jan. 15, 2026 ]

Here is screen-shot of final run result of Martingale Simulator making over 72 million dollars (!), starting with 100,000 dollars, and an initial bet-size of $1000, and a win probability of 0.72 (a very *BIG* edge), and 100,000 trades.

Note the there is now only a drawdown of over 127,000 dollars, and a run of only 7 losses in a row.

If you really have an edge, you can maybe use the Martingale approach, despite it's risks. The key here, is that the 72% probability of win, means the probability of loss is reduced to 28%. If you take 0.28 ** (to the exponent of) 10, you get 0.00000295. And 0.00000295 times 100,000 trails, means you can expect to get only 0.29619 events of 10-losses in a row, which is less than once per 100,000 trades.

Raising the win-probability (and reducing the loss probability), makes a big difference, because you can see the simulator's biggest run of losses was only 7, not 15 like the previous 100,000 trades run. So, with the bigger edge, we can dial up the bet-size, and really goose the process.

A lot of algorithmic-trading market activity now, is probably being driven by this sort of push-it-to-the-limit kind of betting strategy. And what one finds, is that you can flip the idea of the Martingale betting strategy around, and instead of increasing bet size when the process is losing money (to recover loses), you can instead increase the bet size when the algorithmic process has made a win.

The old smart traders did this. When they were right, and on a roll, they *increased* their bet sizes, and added to their trades. When the results went against them, and they were proven by the market to be wrong, they would reduce their bet sizes after closing their losing positions.

I want to simulate this, because I think it is a better strategy to use, in the real world, with real data, where unlimited variance seems to be the case. We can find our "edge" suddenly disappears, right when we need it most!

(Click on image to expand, ESC or click outside image to exit)